What is Number System?
A number system is method of representing the numbers for calculations.
There are two types of number systems.
1) Non-positional number system
2) Positional number system
Different types of positional number system are:
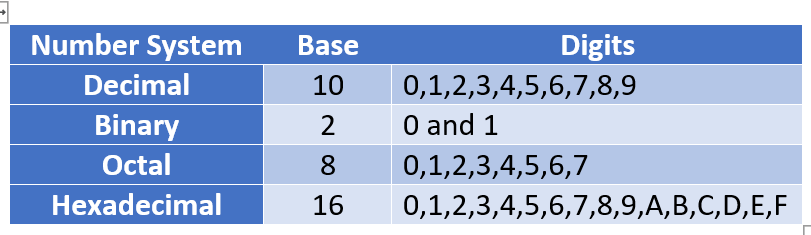
a) Decimal number system
b) Binary number system
c) Octal number system
d) Hexadecimal number system
Decimal number system: – A number system which is used in our day-to-day life. It has 10 digits (0,1,2,3,4,5,6,7,8,9). Therefore, base is 10.
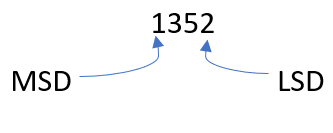
Example: 15(10), 45(10) and 540(10)
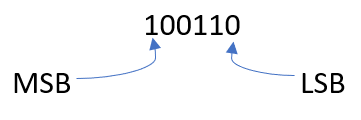
Binary Number System: – A number system which a computer can understand and used for processing of data. It has only two digits 0(Zero) and 1(One). These are Binary digit (BIT). Thus, base is 2.
Example: 10100(2), 111010(2).
Octal Number System: – It has 8 digits (0,1,2,3,4,5,6,7,8). Therefore, base is 8. The octal number have the digits between 0 and 7.
Example: 512(8), 3412(8)
Hexadecimal number system: – It has 16 digits. These digits are (0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F). Therefore, base is 16. Where 10=A, 11=B, 12=C, 13=D, 14=E and F=15.
Conversions
Decimal to Binary
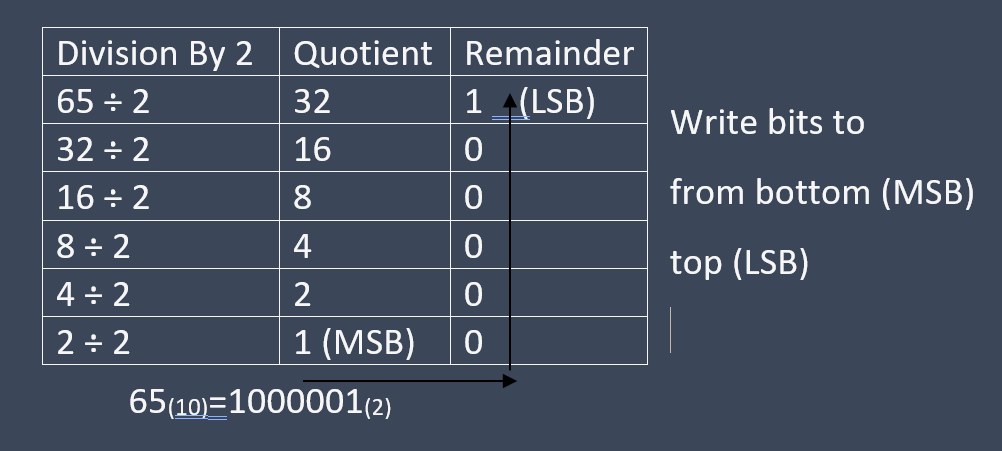
Step 1: Divide the given decimal number by 2
Step 2: Note the quotient and remainder
Step 3: Repeat above two steps until quotient becomes zero
Step 4: Remainder from the first step is called is LSB and from last step is called MSB. Write all remainders together from MSB to LSB.
Example 1: Converting decimal number 25 to binary number system.

Example 2: Converting decimal number 65 to binary number system.
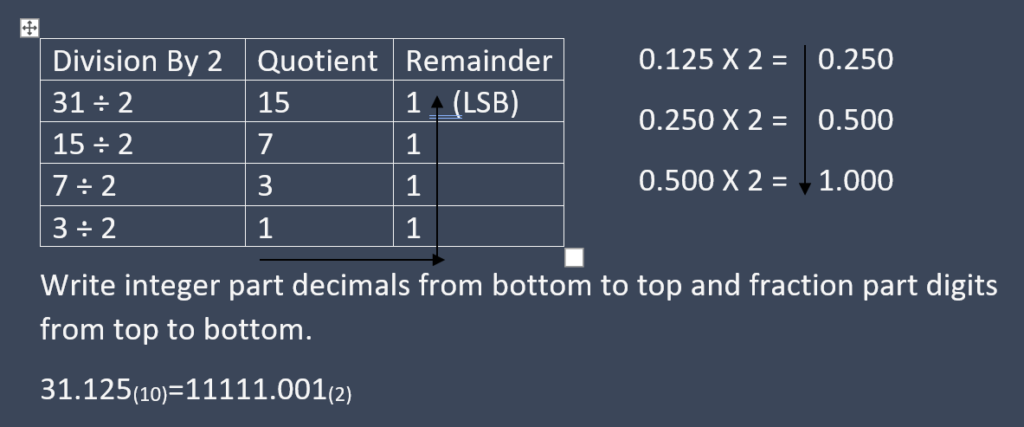
Decimal fractions to binary: In this, given fractions are repeatedly multiply by 2 until fraction part becomes zero or number of digits approximation according to the needs. Finally keep all those digits present in integer part from top to bottom.
Example 31.125
Binary to decimal number system
Step 1: Multiply each bit of binary number with its positional weight.
Step 2: Add all product terms
Example: Convert 101100(2) to decimal number system.
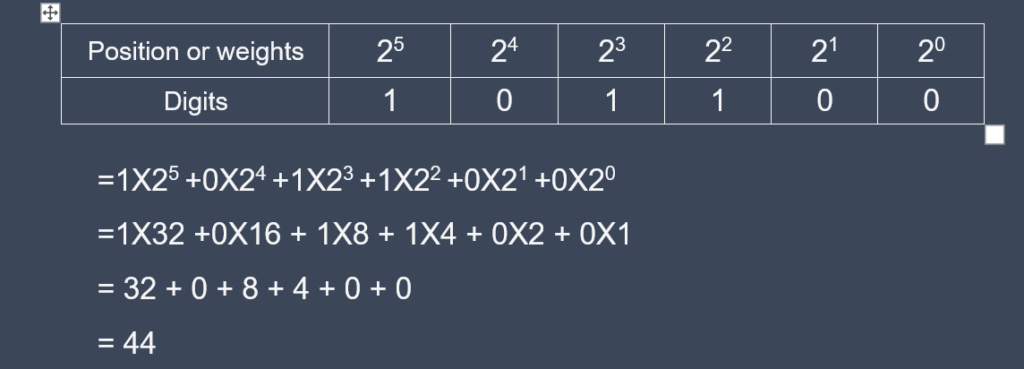
Decimal to Octal conversion
Step 1: Divide the given decimal number by 8
Step 2: Note the quotient and remainder
Step 3: Repeat the above step until the quotient becomes zero.
Step 4: Remainder from first step is LSB and from last step is MSB. Write the remainders together from MSB to LSB.
Example: Convert 532(10) to octal number

Octal to Decimal conversion
Step 1: Multiply each digit of an octal number by their weights
Step 2: Add all the product terms.
Example: Convert 5216(8) to decimal

Decimal to Hexadecimal conversion
Step 1: Divide the given decimal number by 16
Step 2: Note the quotient and remainder
Step 3: Repeat above steps until quotient becomes zero
Step 4: Remainder from first step is LSB and from last step is MSB. Write the remainder together from MSB to LSB.
Example: 4096(16)=(?)

Conversion of Hexadecimal to decimal
Step 1: Multiply each digit of hexadecimal number by its positional weight
Step 2: Add all product terms.
Example: Convert 2BA(16)=(?)10

1’s Complement
A method of replacing of 1 into 0 and 0 into 1 in a binary number is called 1’s complement system. It has two steps.
Step 1: Convert given decimal number into binary number
Step 2: Replace 0 into 1 and 1 into 0.
Example 1: Find 1’s complement of 15
Given 15(10) = 1111
1’s complement = 0000
Example 2: Find 1’s complement of 46
Given 46(10) = 101110
1’s complement = 010001
2’s Complement
A method of finding 1’s complement for a given number and adding 1 to it is called 2’s complement system.
i.e. 2’s complement = 1’s complement + 1
Step 1: Convert given decimal number into binary number.
Step 2: Replace 0 into 1 and 1 into 0 (i.e. 1’s complement)
Step 3: Add 1 to 1’s complement.
Example 1: Find 2’s complement of 12
Given 12(10) = 1100
1’s complement = 0011
Add 1
2’s complement = 0100
Example 2: Find 2’s complement of 72
Given 72(10) = 1001000
1’s complement = 0110111
Add 1
2’s complement = 0111000
Binary arithmetic’s
Rules for binary addition
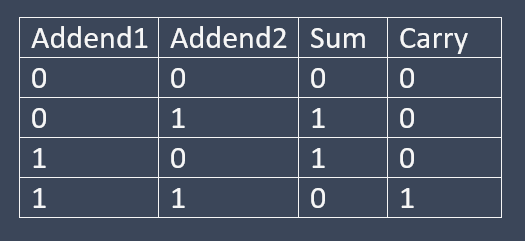
Addition of 3 bits (1+1+1) is given below

Rules for binary subtraction
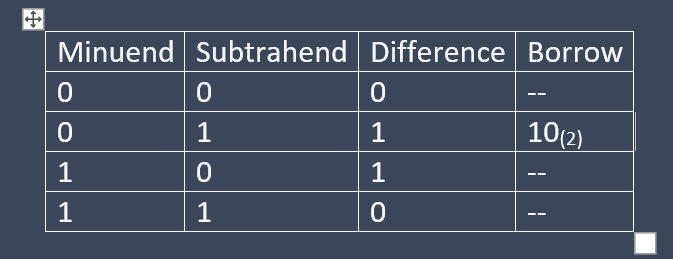
Example: (minuend) 10 = 1010
(subtrahend) 5 = 0101
Difference 5 = 0101
Subtraction using 1’s complement system
a) Subtraction of smaller number from bigger number
Step 1: Find the one’s complement for a subtrahend
Step 2: Add one’s complement pf subtrahend to minuend
Step 3: If any carry occurs, add that to LSB of sum.

b) Subtraction of bigger number from smaller number
Step 1: Find the one’s complement for a subtrahend
Step 2: Add one’s complement of subtrahend to minuend
Step 3: If any carry occurs, add that to LSB of sum
Step 4: Find the 1’s complement of the result

Subtraction using 2’s complement system
a) Subtraction of smaller number from bigger number
Step 1: Find the 2’s complement for a subtrahend
Step 2: Add 2’s complement of subtrahend to minuend
Step 3: If any carry occurs, discard it.

b) Subtraction of bigger number from smaller number
Step 1: Find the 2’s complement for a subtrahend
Step 2: Add 2’s complement of subtrahend to minuend
Step 3: If any carry occurs, add that to LSB of sum
Step 4: Find the 2’s complement of the result.
